The relationship between culture and cognition / language
Much of what we currently know about cognition is based on data from WEIRD people: Western, Educated, Industrialized, Rich and Democratic people (Henrich, Heine & Norenzayan, 2010). If we want to know the origin of various cognitive abilities (such as number cognition and language), we need to examine more than just industrialized cultures, such as English, Russian, Chinese and Japanese. A major research focus in the lab consists of investigating cognition in remote cultures, such as the Pirahã (an indigenous population in the Brazilian Amazonian region) and the Tsimane’ (an indigenous population in the Bolivian Amazonian region). We investigate number cognition and its ramifications on other parts of cognition, and language.
Number cognition: Pirahã
Frank, Fedorenko, Everett & Gibson (2008, Cognition)
Before our work on the Pirahã, it was thought that all cultures had the ability to represent large exact numbers.
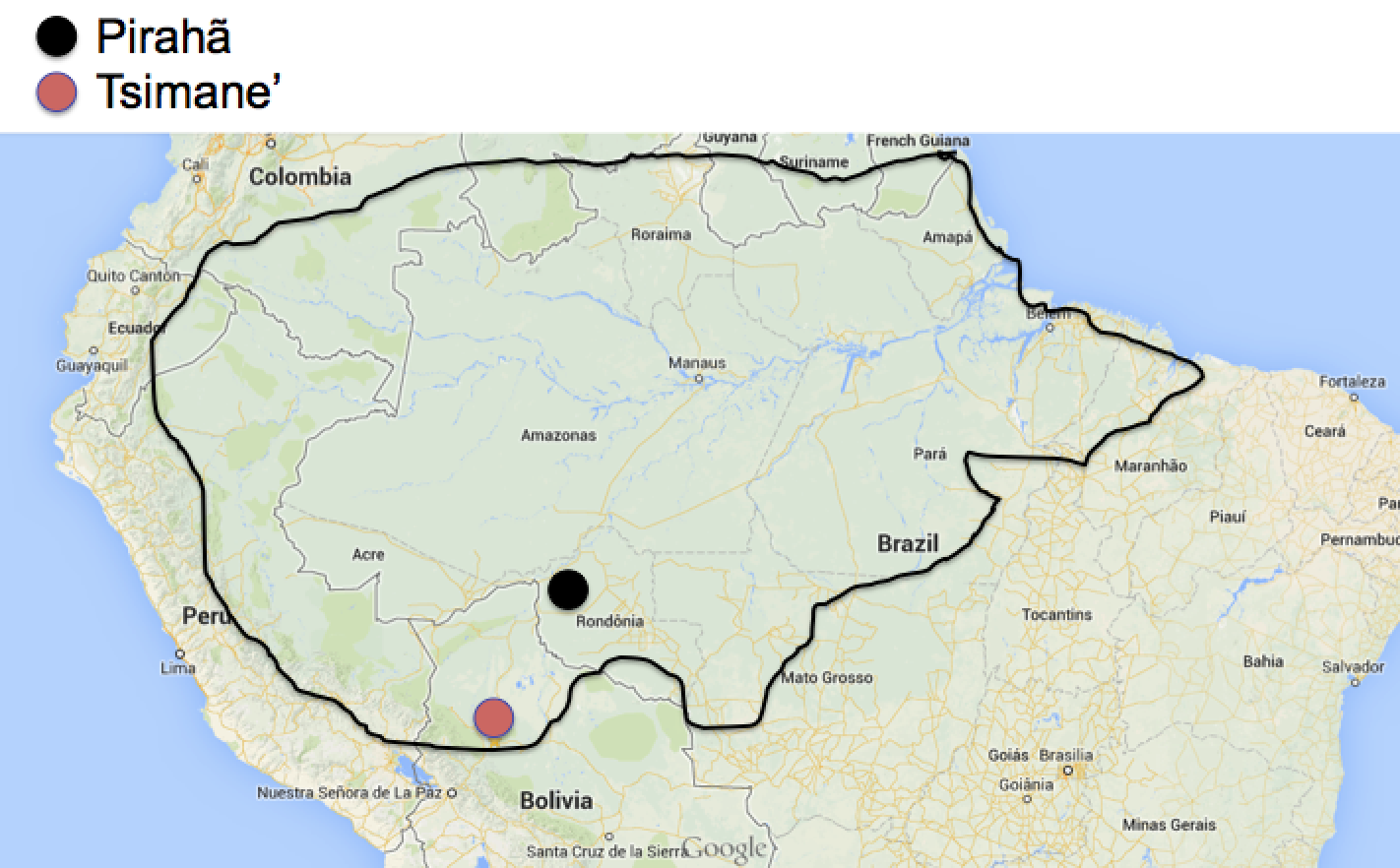
One of the first experiments that we did with the Pirahã was a simple task involving counting up and counting down, using a bunch of identical objects for the participants to count / quantify. Researchers before us had thought Piraha was a 1/2/many counting language, meaning that it was thought to have three words that indicate the count words 1, approximately 2, and many. The words in Piraha had been identified by Dan Everett as hoi’ (1), ho’i (~2) and bagisu (many) (see also Gordon, 2004). In our task, we used spools of thread to be counted, because (1) we had a large set of identical spools of thread with us; (2) the Pirahã were familiar with these objects; and (3) they were easy to manipulate. In the task, we would first put one spool of thread on the table and ask the participant to describe what this was. They would say “hoi’ thread”, where we thought the word hoi’ meant “one”. We would then put out two spools of thread, then three, then four, all the way up to ten spools of thread, each time asking the participant to describe what was in front of them. We observed, as others had before, that the participants would use the same head noun each time (for “thread”) and only three different quantifiers: hoi’, ho’i, and bagusu. They would use the word we thought was “one” for the singleton set, then they would use the word we thought was “about 2” for sets of size 2-4, and then after 4 they would tend to use the word we thought was “many”.
The interesting part of the task was when we asked participants to do the same procedure, but now starting with ten spools of thread, and working our way back down to one. Here, something very interesting happened: they would start with the word for “many”, but they would quickly start using the word we thought was “about 2” and then they would use the word we thought was “one” at about six objects, and by four objects, everyone used this word. So we got strikingly different results, depending on whether a participant was counting up, or counting down.
We explained this in a simple way: the word we thought was “one” was in fact “few”; the word we thought was “about 2” was in fact “some”, and the word we thought was “many” was “many”. We get the different results across the two presentations because of the contextual differences: with no other items, only one seems like few. But when we start with ten objects, then six, five and four, all of these smaller sets seem like “few” relative to what was there before. Perhaps most interestingly here, we were the first to observe that Piraha has no counting words whatsoever, not even a word for “one”. This is the first instance of researchers making this observation.
Matching and counting tasks
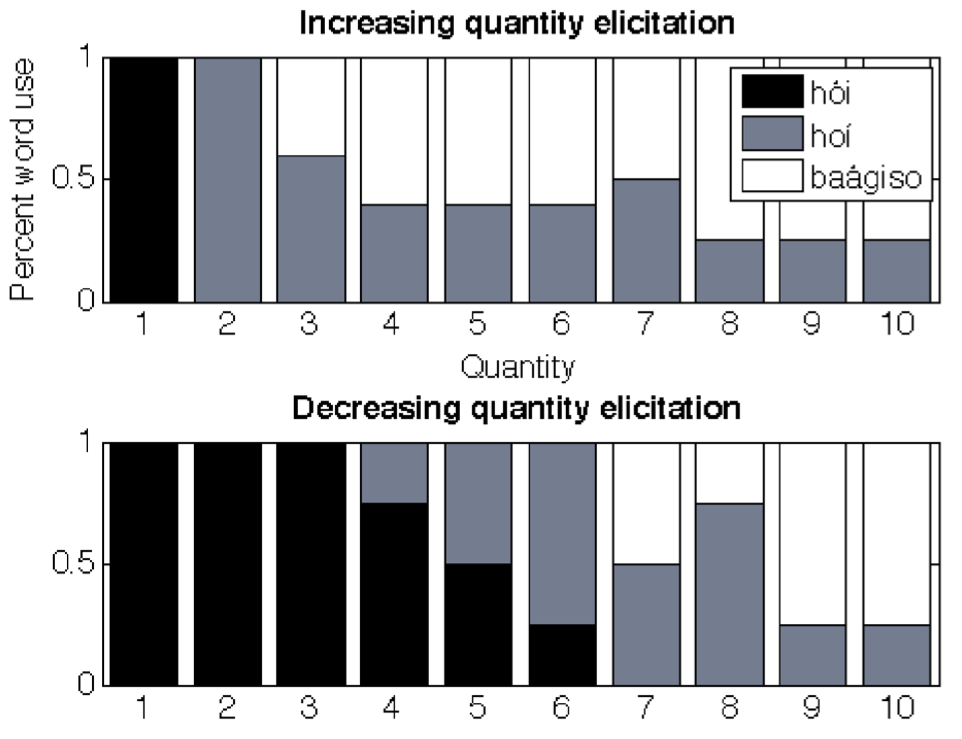
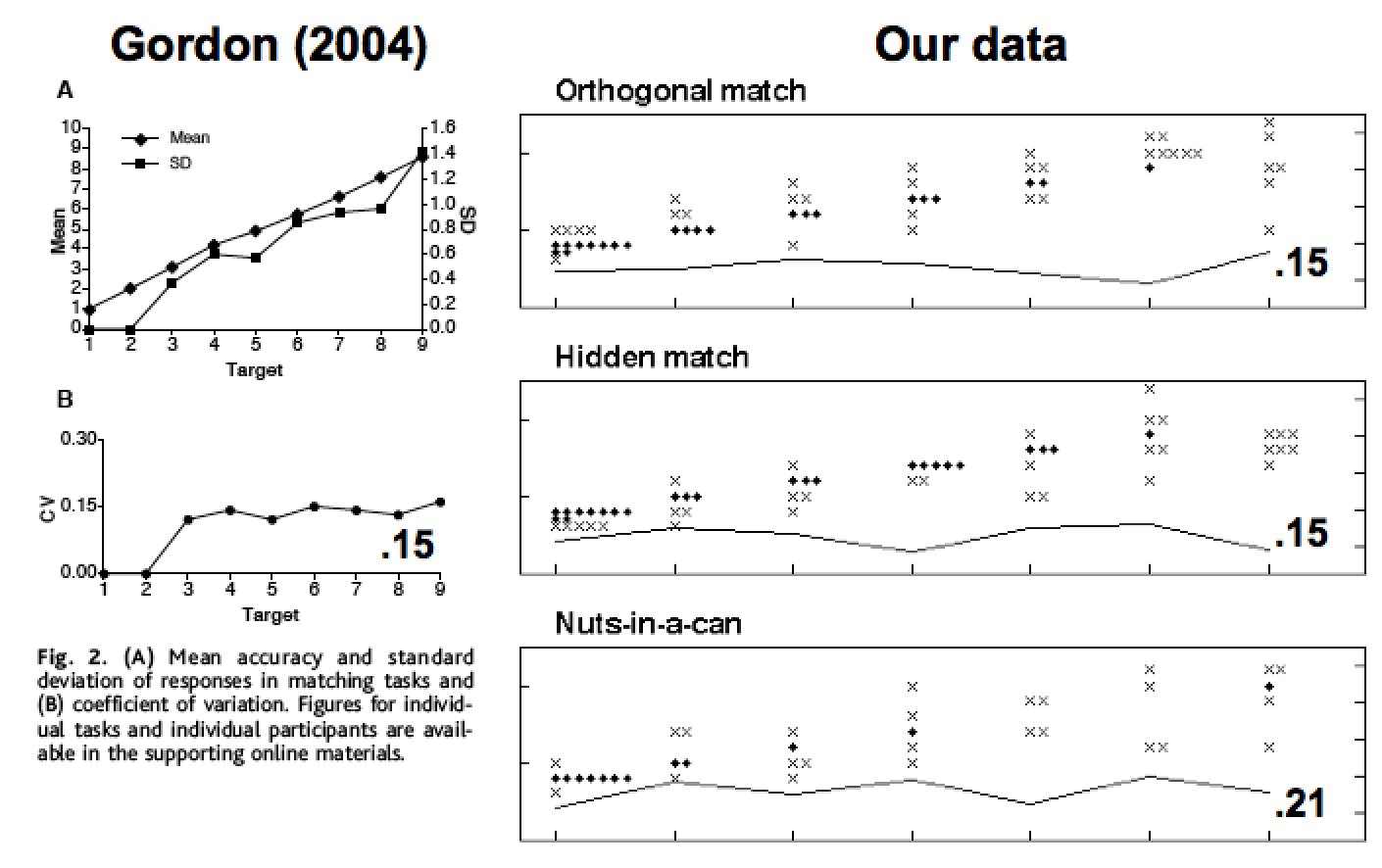
Our next set of experiments sought to test a claim from Gordon’s 2004 Science paper that stated that the Piraha couldn’t do exact matching of items. That is, Gordon had observed that his Piraha participants only did approximate matching of set size, even when the task was 1-1 matching, with no memory component. In the simplest of Gordon’s tasks, he had participants put one of each of their objects (a set of batteries) against a set of objects that the experimenter put out (another set of batteries). Gordon found that the participants did this exactly correctly for small set sizes (for one to about four) but after that, they did the task approximately. Even if the Piraha people can’t count exact numbers, this result is surprising: this task requires no counting ability, only the ability to see if an object already has a matching object. Gordon used this surprising result to argue for a very strong Whorfian hypothesis: that without any words for exact numbers, the Piraha couldn’t even understand the concept of exact matching.
A serious issue with Gordon’s experiments, however, is that there is no way to ensure that the participants understood the task. What if they thought that the task was simply an approximate matching task? This is especially worrisome for Gordon’s results because Gordon didn’t have a good Piraha translator working with him. And in one video that used to be displayed on Gordon’s website when the paper was first published, it seemed like the participants didn’t understand the task, because one is heard saying “he wants you to do it faster”, which is not what the experimenter wanted (Dan Everett, personal communication). Consequently, it was a serious concern that the participants didn’t understand the task.
We re-ran several of Gordon’s tasks, including two versions of the exact matching task. We worked with Dan Everett, who speaks good Piraha, so that the instructions were clear. Furthermore, there were two experimenters (Ted Gibson & Mike Frank), who always demonstrated the task to the participants clearly. In particular, Gibson would first put out 2 objects (spools of thread: the experimenter objects), and then ask Mike Frank to do the task, which was to place one of each of his objects (uninflected red balloons, easily manipulable identical objects) against each of the spools of thread. Mike would do so. Then we would repeat this process for a set of size three. We would then ask the participant to do the same thing as Mike: repeat his actions on the set size two, and then the set size three. If a participant made an error (e.g., putting out only 2 balloons for the set of size 3) then we would correct them, and start over, demonstrating 2 and 3 again, and letting them try a second time. Most participants understood right away, but a couple of participants made an error, and needed a second demonstration. Everyone understood after the second demonstration.
We would then put sets of 2, 3, 4 objects out for matching, then some sets between 5 and 10 items (5, 7, 10 in one group; 6, 8, 9 in the other). Almost all participants got almost all trials correct. There were only 4 incorrect trials in 17 participants’ data. (This is comparable to the number of errors that MIT undergrads made on similar tasks that we ran later (Frank et al. 2012): sometimes people just leave one out by mistake, in their haste, or because they aren’t paying close attention.)
Thus, we did not replicate Gordon’s results: the Piraha participants were able to perform the exact matching task, contrary to Gordon’s claims. Our guess as to why we didn’t replicate his results is that the instructions were probably not clear in Gordon’s task. His participants probably thought that they were doing an approximate matching task rather than an exact matching task.
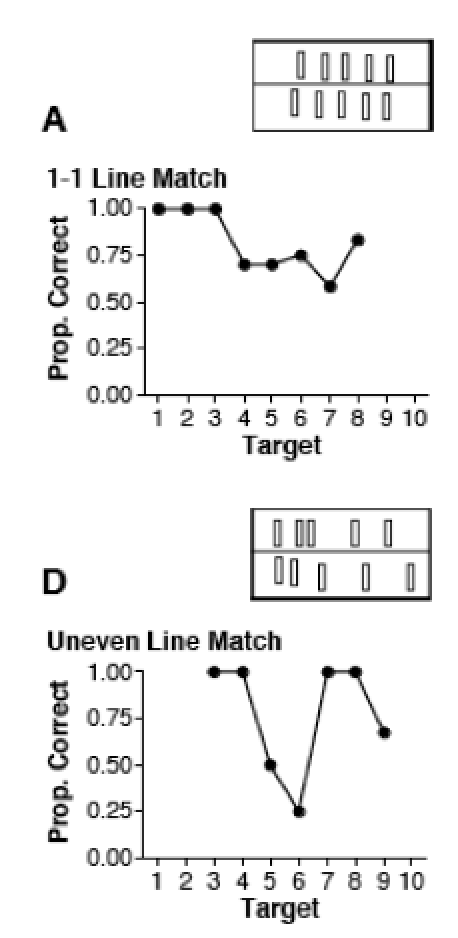
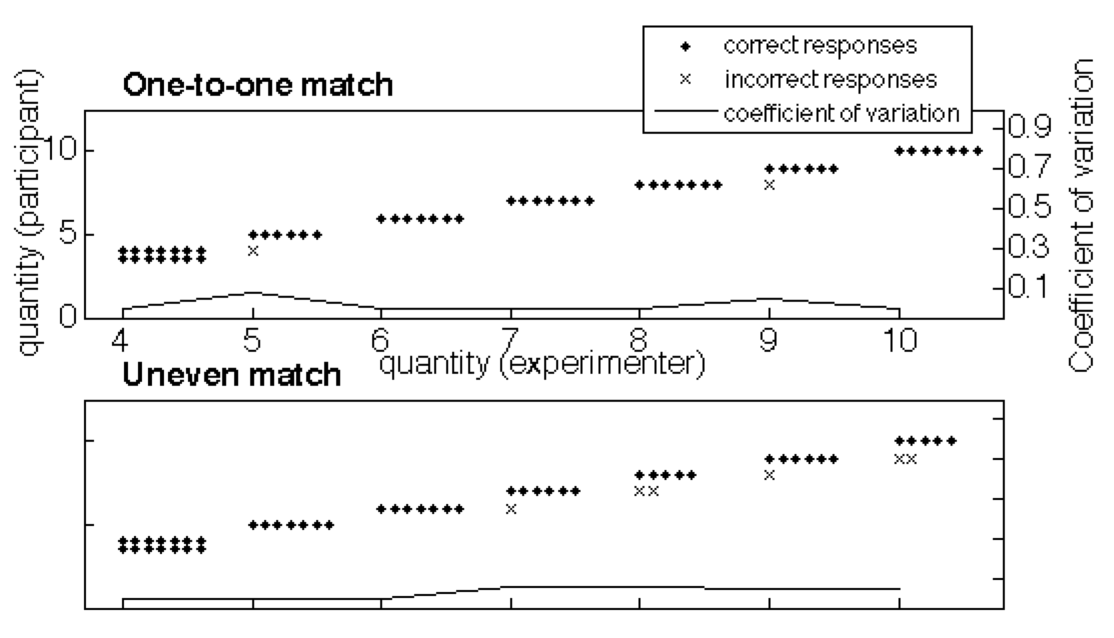
We also re-ran three of Gordon’s exact matching tasks, each of which required some memory resources in order to solve them: (1) A hidden display task, where the set of spools of thread was shown to the participant and then hidden. The task was to put the balloons in front of where the spools were. This task is easy if one can count: the way to keep track of ten spools of thread is to keep track of the number ten, and then put out ten balloons. Without being able to count, however, this is a complex visual memory task. (2) An orthogonal match task, where we put out the set of spools of thread in an orthogonal line, away from the participant. In this task, the participant would continue to put out his/her balloons in the same horizontal pattern as in other tasks. This task is most easily solved by counting and then putting the same number. (3) A “nuts in a can” task, where we would put the spools of thread one by one into an opaque mug. The task was to put the same number in a horizontal line in front of the participant, in the same orientation as in all other matching and counting tasks.
Like Gordon, we found that Piraha participants performed these tasks as if doing approximate matching. They were always correct on 2 and 3, mostly correct on 4, and made more errors as the numbers got larger, but they always put out the approximately right number. This result ends up being unsurprising now that we know that there are no count words in Piraha, so that the task must be solved approximately.
Video of a Piraha participant doing a counting task: succeeding with a small number Video of a Piraha participant doing a counting task: failing with a large number (10)
Interestingly, C. Everett & Madora (2012, Cognitive Science) were able to successfully replicate Gordon’s (2004) results, finding that their Piraha participants did not perform an exact matching task, even on a task with no memory requirements. C. Everett & Madora concluded that the participant group that we ran in Frank et al. (2008) may have benefitted from learning to count from Dan & Keren Everett’s training, years earlier. C. Everett & Madora claimed that their participant group had received no such training, and therefore couldn’t do the exact matching task. However, there are some serious problems with this interpretation. First, there was no independent evidence that the participants run by Frank et al (2008) knew how to count. None of them knew any count words, and they all did the counting tasks using approximate number. Not one of them could perform any of the counting tasks. Second, because they performed the matching tasks as approximate matching tasks, there is no way to know that they actually understood the intended instructions. It is only when they succeed on these kinds of tasks that we can interpret the other results. When they fail this task, it is possible that they understood the task to be an approximate matching task.
See also Frank et al. (2012) where we show that English speakers behave somewhat like Piraha speakers on exact matching tasks, when their verbal resources are occupied. This shows that the existence of an exact counting system does not replace the approximate matching system: it is used when it is most useful.
Number learning: Tsimane’
Piantadosi, Jara-Ettinger & Gibson (2014, Developmental Science)
We first traveled to Bolivia to work with the Tsimane’ in 2012. In one of our first experiments there, we investigated how children learn number words. Unlike Pirahã, Tsimane’ has number words for 1-100. Beyond 100, they use Spanish words. An interesting question is how these number words are learned. It has been shown that children in industrialized nations learn to count between 3 and 4 years old. First, it seems like they learn the count list (“one, two, three, four, five, six, seven, eight, nine, ten”), then they learn the meanings for these words. A classic method of testing what number meanings kids know is the give-N task (Wynn, 1992). In this task, a participant is given a set of identical objects: we used 8 American quarters, on a sheet of white paper. Then the participant is asked to give some number back. E.g., give one, give two, give five, etc. A participant is said to be a 1-knower if they correctly return one object when asked for one, but consistently fail on higher numbers. A participant is said to be a 2-knower when they can do one and two, but not three or higher. Interestingly, it appears that children in industrialized nations go through a stage of being a 0-knower (where they fail on all give-N numbers), then go through a stage of being a 1-knower, then a 2-knower, then a 3-knower, sometimes a 4-knower, and then know all the numbers up to ten (and sometimes more, depending on how well they know the count list). Most interestingly, there is never a 5-knower: a child that understands 1, 2, 3, 4 and 5, but not 6 and 7 and 8. This fascinating result has suggested to researchers that some inference takes place at this stage. Piantadosi et al (2012) provide a model in which the learner is provided with knowledge of sets, and knowledge of the meanings 1, 2, and 3, and knowledge of the count list. This learner is then exposed to pairs of words for numbers and their cardinalities (how many are in a set), and it learns the count list in much the same way that children do: going through the stages of 0-knowing, 1-knowing, 2-knowing, 3-knowing, sometimes 4-knowing, and then jumping to understanding the meaning of all the numbers in its count list.
An open question for this research program had been whether it is the amount of data that solely determined the order of number learning, or whether the age of the child and hence their working memory ability might interact in some way. In particular, it was an open question whether children who were exposed to less counting data might go through different stages of number learning, perhaps missing the 3- or 4-knower stages, or even going through 5- or 6-knower stages. Our work with the Tsimane’ addressed this question. While the Tsimane’ have exact number words, these words are probably much less frequent in their typical usage than in industrialized countries, because the Tsimane’ culture is a farming-foraging culture which does not rely much on counting.
Interestingly, we found that the Tsimane’ children go through the very same stages of number learning as children in industrialized countries, just delayed a few years. In particular, there are still 0-, 1-, 2-, 3- and 4-knowers in Tsimane’, but no 5- or 6-knowers. Children learn to count in the same stages, but learn their counting skills at an average age of 8 rather than 3-4, as in industrialized countries. This result shows that it is the amount of data that is relevant to the learning task.
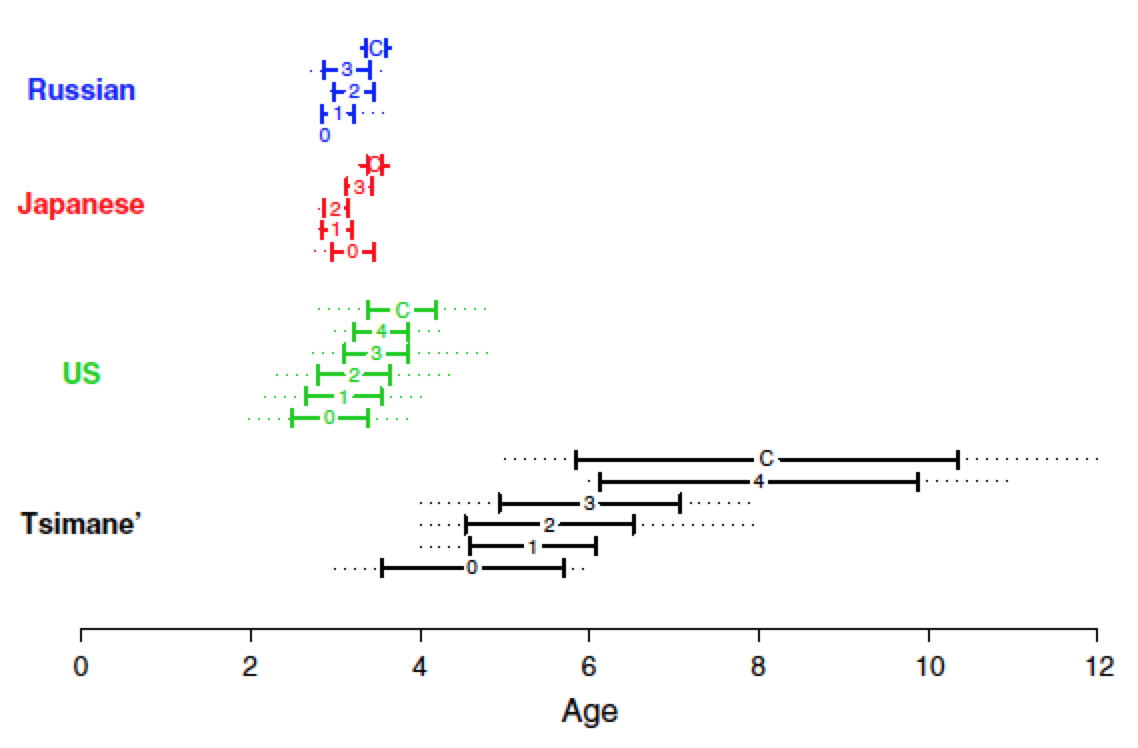
Figure 1. The age ranges of different subset-knower levels from a variety of previous studies (US, Japanese, and Russian), compared to Tsimane’ children. The solid ranges show the mean ages plus and minus one standard deviation; the dotted lines show the minimum and maximum ages for each level. This demonstrates a substantial delay in the course of development, on the order of 2~6 years, for Tsimane’ children. (Thanks to Meghan Goldman and Barbara Sarnecka for compiling and sharing the data from the industrialized populations.)
Mastery of the logic of natural numbers is not the result of mastery of counting: Evidence from late counters
Jara-Ettinger, Piantadosi, Spelke, Levy & Gibson (in press, Developmental Science)
In order to master the natural number system, children must understand both the concepts that number words capture and the counting procedure by which they are applied. These two types of knowledge develop in childhood, but their connection is poorly understood.
In this project, we explored the relationship between the mastery of counting and the mastery of exact numerical equality (one central aspect of natural number) in the Tsimane’. Critically for the project, Tsimane’ children master counting at a delayed age and with higher variability relative to children in industrialized societies. By taking advantage of this variation, we sought to better understand how counting and exact equality relate to each other, while controlling for age and education. We found that the Tsimane’ understand exact equality at a delayed age, correlating with the time when they learn number words and counting, controlling for age and education. However, some children who have mastered counting lack an understanding of exact equality, and some children who have not mastered counting have achieved this understanding. These results suggest that understanding of counting and of natural number concepts are at least partially distinct achievements, and that both draw on inputs and resources whose distribution and availability differ across cultures.
Applications of learning to count: Different notions of fairness
Jara-Ettinger, Gibson, Kidd & Piantadosi (2015, Developmental Science)
Cooperation often results in a final material resource that must be shared, but deciding how to distribute that resource is not straightforward. A distribution could count as fair if all members receive an equal reward (egalitarian distributions), or if each member’s reward is proportional to their merit (merit-based distributions). In this project, we evaluated whether the acquisition of numerical concepts influences how we reason about fairness. We explored this possibility in the Tsimane’, a farming-foraging group who live in the Bolivian rainforest. The Tsimane’ learn to count in the same way children from industrialized countries do, but at a delayed and more variable timeline, allowing us to de-confound number knowledge from age and years in school. We find that Tsimane’ children who can count produce merit-based distributions, while children who cannot count produce both merit-based and egalitarian distributions. Our findings establish that the ability to count—a non-universal, language-dependent, cultural invention—can influence social cognition.
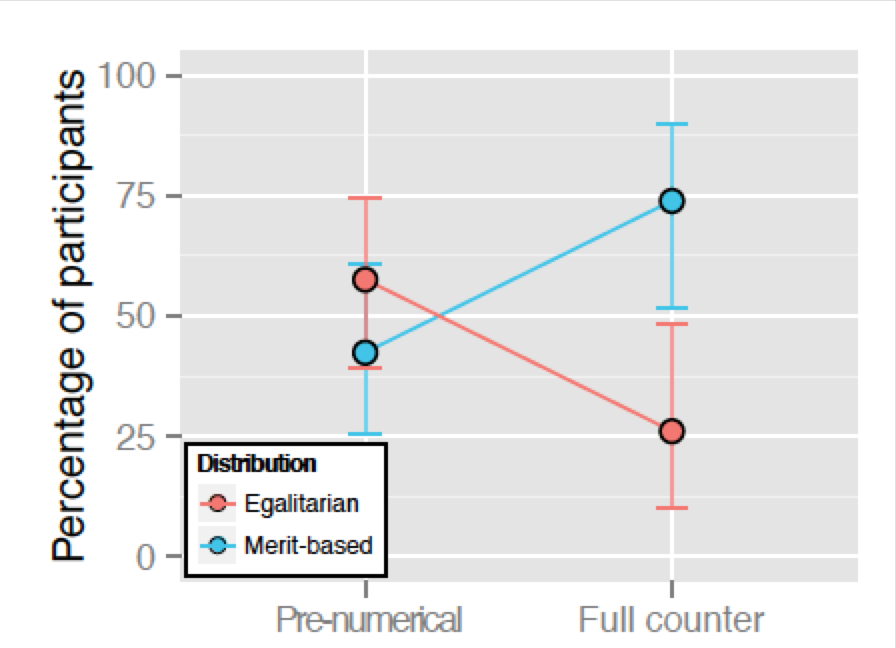
Figure 1: Children who cannot count (pre-numerical) show no overall bias between egalitarian and merit-based distributions. In contrast, children who can count (full counters) are biased towards producing merit-based distributions, giving more cookies to the harder working child. Each point shows the proportion of children making each choice and the vertical bars show 95% confidence intervals on the estimate.
Computerized experiments may underestimate cognitive abilities in non-industrialized populations
Gibson, Jara-Ettinger, Levy & Piantadosi (under review, Cognitive Science)
In order to understand the universal properties of human thought, there has been a burgeoning interest in cross-cultural research focused on remote, non-industrialized cultures (Henrich, Heine & Norenzayan 2010). However, differences in behavior must always be interpreted with care, as culture often unexpectedly influences performance in ways that challenge interpretation. For instance, during a research trip to the Pirahã in 2007, our research team attempted to run a simple number judgment task in which participants were asked to choose between two piles of candies with slightly different numbers (e.g., 5 vs. 6 candies). The task did not translate well: each of four independent pilot participants first asked us what other goods we had. We told them that for the purposes of the task, they should focus only on the candies on the table. All four participants persisted in asking us what else we had: three of the four wanted to know if we had any perfume (they had encountered perfume from river traders). We tried to explain the task again. All of them then asked – very reasonably – why they couldn’t have all the candies. We explained the task again, and it became clear that none understood what we wanted or why one might ask someone to choose between two piles of candies. Each participant completed the task by simply taking the pile closest to them.
Such experimental problems, in some sense, are not as problematic as more subtle failures where cultural factors and expectations may influence outcomes in ways that experimenters may not notice. Recently, we began to explore how the ability to perform exact arithmetic and the ability estimate approximate quantities (e.g., Halberda et al 2008) are related in the Tsimane’. The Tsimane’ are a native Amazonian group living in the lowlands of Bolivia (Huanca, 2008). They live in small groups, hunt, and farm (to a limited extent) for subsistence. Unlike people from industrialized countries, many Tsimane’ adults have never attended school at all, and those that have attended often begin school at a later age than corresponding individuals in industrialized countries, and they leave school earlier. Hence their education level is highly variable across the population. Our pilot studies —conducted on a computer— revealed that the Tsimane’ had a surprisingly poor ability to approximate set sizes (high Weber ratios, W) compared to participants from the US. Although subjects seemed to understand the task well, and were certainly not performing at chance, some subjects seemed uncomfortable with the computers used to present dot arrays. Based on these intuitions we decided to investigate whether the use of a computer interface affected their performance.
To explore this possibility, we ran an approximate number task in a native Amazonian population using two presentation methods: (1) using a computer interface; and (2) using physical cards. The displays looked like the figure below, and the testing procedure was very similar across the two tasks. Participants simply had to touch one of the squares below the presented figure (red or black) corresponding to the set of dots with the greater number. For the computer task, participants would touch the red / black box on the screen below the dot display. For the card task, participants would touch the red / black box on the table in front of them, below the dot display.


An example stimulus consisted of black and red dots of varying sizes, intermixed inside a disc. Participants were asked to touch the black square if there were more black dots, or the red square if there were more red dots.
Participants with three or more years of schooling performed equally well on both versions of the task, but participants with zero, one or two years of education performed significantly worse on the computer-based task. These results highlight the importance of task considerations when working with non-industrialized cultures, especially those with low education. Using computers may lead researchers to find spurious population differences in such measures.
Shape bias
Jara-Ettinger, Piantadosi, Levy, Sakel & Gibson (in preparation)
Understanding what new words refer to is a central problem when learning a language. In the US, children believe that objects, but not substances, are named on the basis of their shape (Landau, Smith, & Jones, 1988). Nevertheless, the strength of this shape-bias varies across cultures. Empirical evidence suggests that the shape-bias is influenced by the speaker’s language (See Imai & Mazuka, 2001 for review): Languages that distinguish objects from substances through their syntax and morphology (such as English) help speakers acquire an object shape-bias. In contrast, languages that treat objects and substances identically (such as Japanese) prevent speakers from acquiring a strong shape-bias.
Here we propose that in addition to language, environmental factors underlie how we name objects (cf. Bloom & Keil, 2001; Prasada, 1999). In industrialized cultures we mostly interact with artifacts that have systematic shapes, but variable color and texture. As such, shape, but not color or material, is indicative of their key properties. However, an object’s color or material may be indicative of its category if these features seem non-accidental. This predicts that non-industrialized cultures with fewer artifacts should find uncommon colors or materials to be as indicative of an object’s category as its shape. To explore environmental influences on object naming we tested how the Tsimane’ – an indigenous Amazonian group from lowland Bolivia – generalize object names.
First, we ran two language acceptability tasks with Tsimane’ adults (N=31) to test if their language has syntactic or morphological markers to distinguish objects from substances. Our first task showed that the Tsimane’ judge that it is acceptable for count words to directly modify objects (e.g., one house) but not substances (e.g., *one mud). Our second task showed that the Tsimane’ believe it is more acceptable to add a plural marker to objects (e.g., many houses) than to substances (e.g., *much muds). Having established that Tsimane’ has an object-substance distinction enables us to test cultural effects on object naming while controlling for the effects that object-substances markers may have.
Next, we ran a word extension experiment where participants learned an object’s name and were asked to generalize it to a new object from a set. First, we confirmed that US adults and children prefer to generalize an object’s name to other objects with the same shape in the presence of color- and material-matching alternatives (Experiments 1 and 2; N=144 and =30, respectively, p<0.01 in both cases). In contrast, Tsimane’ adults (Experiments 3 and 4; N=80) were equally likely to extend an object’s name to the shape-, the color-, or the material-match. However, they were significantly less likely to extend the object’s name to objects with no common features (p<0.01). Similarly, Tsimane’ children (Experiments 5- 7; N=109) were not biased towards any of the matches, but they avoided generalizing names to objects with no common features (p<0.001).
Our results show that having an object-substance distinction is not sufficient for speakers to acquire a shape bias. Instead, cultural factors influence how speakers generalize the meaning of words. As such, the shape-bias appears to be the result from learning non-accidental features of objects (see Prasada, 1999).
Color words
Forthcoming.
The syntax of Pirahã: Does Pirahã contain recursive structures?
Futrell, Stearns, Piantadosi, Everett & Gibson (in press, PLoS)
The Pirahã language has been at the center of recent debates in linguistics, in large part because it is claimed not to exhibit recursion (Everett, 2005), a purported universal of human language (Hauser, Chomsky & Fitch, 2002). In this project, we present an analysis of a novel corpus of natural Pirahã speech that was originally collected by Dan Everett and Steve Sheldon. We make the corpus freely available for further research. In the corpus, Pirahã sentences have been shallowly parsed and given morpheme-aligned English translations. We use the corpus to investigate the formal complexity of Pirahã syntax by searching for evidence of syntactic embedding. In particular, we search for sentences which could be analyzed as containing center-embedding, sentential complements, adverbials, complementizers, embedded possessors, conjunction or disjunction. We do not find unambiguous evidence for recursive embedding of sentences or noun phrases in the corpus. We find that the corpus is plausibly consistent with an analysis of Pirahã as a regular language, although this is not the only plausible analysis.